The complement is another encoding of the opposite of the original number of positive numbers. It can make up the positive number in the word length to be all zero.
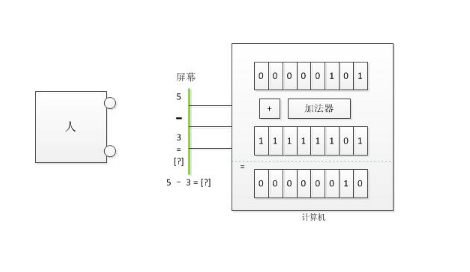
The meaning of the complement:In real life, we have addition, subtraction, multiplication, and division, but there is only one adder in the computer. In other words, the addition can be done directly in the computer, and the subtraction, multiplication, and division operations must eventually be converted to additions. To put it here, some beginners may think why the computer does not design an adder similar to the "adder." The main reason for the "subtractor" or "multiplier" component is that it seems complicated and difficult to implement in a very simple way in life. If you use an adder, you can implement other operations. Other "adders", "subtractors" or "multipliers" are not necessary, which also makes the design of the circuit simpler. Ok, now I briefly talk about the meaning of the complement in the computer. The computer can't directly do the subtraction. The corresponding subtraction must be added to the calculation. However, we found that subtracting another number from one number is the same as adding one number to the "complement of another number". This is what complement does to the computer: it turns the subtraction into an addition.
The complement of a positive number is the basic body
The complement of the negative number is the original code bitwise plus 1
The sign bit is the highest bit, the first bit to the left; the other bits are the remaining 7 bits.
Because the addition of the operator is the fastest, the use of complement is to speed up the calculation.
The code "and the number" are two things.
We usually say or write a "number", usually in decimal, with 10 different "codes" (the "code" here is also different from the original code complement code). It is 0~9. More than 9, which is larger than the largest code, is represented by the carry. So there is the concept of "bit". That is, one place, ten, one hundred, and so on.
When a negative number is expressed, a minus sign is added to the number in order to be compatible with the minus or difference between the arithmetic and algebraic symbols.
This method of writing a number can also be named as a coding method. In this encoding mode, each number has a certain "digit number", that is, "length". A certain number of bits are specified in the computer as "word length", such as 4 bits, 8 bits, 16 bits, 32 bits, and so on. However, the physical storage data of the computer is binary. We humans still prefer to use the decimal method. Moreover, we humans generally do not encounter the concept of "word length" when writing numbers. But when reading numbers and recording data, there is a little something related to the word length. For example, Western loves to divide the data into three groups of three, which is a good memory. For example, 12'000 is read as 12 thousand. Our Chinese love to use "10,000" as the word length, 1'2000, and read 12,000. This example shows that the concept of word length is not very appropriate. Because this is just an expression habit for people. But for the machine, the "word length" is the unit of length of the calculation. To design the computer for the simplest addition, the first thing to consider is that the adder performs an addition. How long is the number of bits? How many bits of adder is the adder designed? and many more. This is the word length of the computer. Together with the coding method, it forms the basis of the computer's calculation.
With the concept of word length, it is better to say complement.
There is also a concept of complement in decimal. To insert a sentence, when it comes to complements, you must first determine the length of the word length.
Complement is an encoding method used to represent negative numbers. Also in order to avoid the subtraction operation in the design of the core adder part of the computer, avoid storing negative numbers when storing data.
For example, let's simulate a decimal computer with a 4-bit length. (assuming there is a mechanism that can have 10 stable states on 1 bit)
Summing two numbers: 1234 and -1234
If the original code is used, then we need to use a 1-bit register to store and represent the negative sign. Suppose that the negative sign is indicated by 1 before the highest leftmost bit of the 4 digits, and 0 is a positive sign.
Then, the original code represents the above two numbers:
0 1234
1 1234
Then the computer does the summation and the process of addition. The computer found that one of the numbers is a negative number, so it is switched to a two positive subtraction mode to operate. This is very inconvenient.
So, the complement is thought of.
Is the addition of -1234 and positive 1234 not equal to 0000? The number among the 4-bit word lengths and 1234 are added to 0000. Is it the only one? It is obvious that the addition of 8766 and 1234 is equal to 1'0000, and the last 4 bits are 0000.
Then, 8766 can look at a coded representation of -1234, called "complement code."
Therefore, the complement code is to encode the number 1234 in a word length to complement the number of 1'0000. That is, the opposite of a positive number, expressed in the computer.
With the sign bit, the complement of the opposite of the positive number 0'1234 is 1'8766.
In decimal, the inverse of -1234 is 1'8765
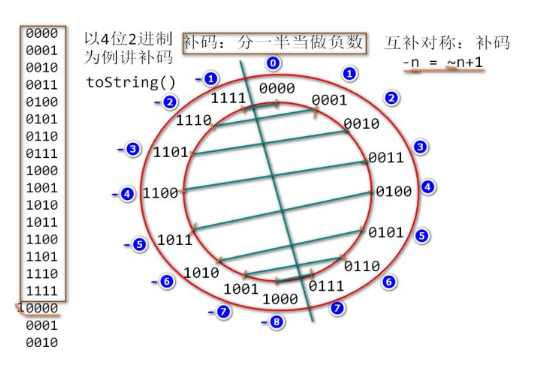
So, let's go back to the 4-digit computer with a 4-bit word length. Complement and inverse are constructed in the same way. The opposite of 0'0001 is -1.
Complement code indicates 1'1111
The inverse code indicates 1'1110
Who invented the unknown, but according to wikipedia, it was originally introduced to the computer by Von Neumann.
A long time ago, the internal numerical encoding of many computers used the inverse. The inverse of this object has its disadvantages: it has -0 and +0 in its range, and a number is added to its complement to -0, which gives the operation Bring some trouble.
There is no such problem with the complement, not only a zero, but the addition, subtraction and multiplication of the complement can be reduced to a way of addition. So the complement in the computer has a great effect on simplifying the operator.
Review of Complementary Codes and Reflections on the Ideas of Complementary Code InventionsComplement and complement definition
N binary bits, M=N-1
Through a coding map. 100. .00 - 111. .11 means (-2^M) - (-1) ; 000. .00 - 011. .11 means (0) - (2^M - 1)
For the complement of code A, f(A) = (2^N)- A
Convert the original code into a complement:
For positive numbers and zeros, the original code is the complement
For negative A, the general understanding of the method:
First do the inverse, then add 1 to the code meaning
The meaning of the complement operation:
In other words, if a number A is negated, a complement operation f(A1) is performed on the complement A1 of that number, and the complement B1 obtained is the complement of the opposite number B of the original number A.
Here is another way to understand the conversion of the original code into a complement.
For the complement of the negative number A
Essentially, the opposite of the negative number A, B, is a positive number, the original code B1 of B is the complement of B, and the complement of A is f(B1)
---
Machine implementation:
Xy = x-1-y+1 = (x-1) - y + 1
In the complement transcoding, here x=2^N
Here, (x-1) - y can be refreshed simultaneously in the ALU even if the y is reversed.
As for the N-bit integer +1, there is a certain carry delay.
---
Boundary situation:
Easy to see, we negate the -2^N, still -2^N
Inverted against 2^N-1, it is -(2^N)-1
---
The use of complement coding
f(y) = -y
x + y = x + y
x - y = x + f(y)
---
After the horse: After the guess, the idea of ​​the complement code is invented, so that the advantage of the complement is seen.
First look at the positive code, let N = 4, -1 = 1001; -2 = 1010, -1 》 -2, but 1001 "1010, the coding order of the two mappings is inconsistent
Inverse, -1=1110, -2 = 1101, Ok, the order is correct,
However, there is a problem here, that is, between a positive number and a negative number, there is a gap of 1. -1=1110, 1=0001, from the perspective of cyclic coding, the two codes differ by 3:1110-"1111-"0000-"0001.
Because positive zero and negative zero are two numbers, the two numbers are broken. How to do? Let the negative numbers move closer to the positive numbers, go further (+1), and lose 1 is gone.
This is the process of making up. Add 1 to the inverse.
I think that when I wrote the big code of the computer's coding design paper (it seems to be Turing or something), of course, there are deeper considerations. However, from the perspective of order and number system, the invention of complement is quite reasonable. And this rationality, I personally think, is its merits.
From the perspective of machine implementation, it is not complicated, but the machine implementation of the opposite code is still more than +1 carry delay.
---
Thinking about int and unsigned int
By the way, I also sorted out the misunderstanding here.
If the variable a is declared as int, but it is treated as unsigned int, if the normal accumulation is out of range, the result of converting to unsigned int should still be trusted.
But forget it, we take advantage of the consistency of the conversion and the type of guarantee, we are still transparent as well.
AC (Alternating Current) Power cord is to transmit high voltage. It is used to drive machinery or home appliances. Since AC Power Cord is output of high voltage electric power, there is a risk of electric shock injury, therefore, All the AC power cord must comply with safety standard to produce. DC (direct Current) power cord is used to the applicance with lower voltage mostly, so safety requirement is less stringent.
Power Cable, battery cable, DC power cable, AC power cable, power cord
ETOP WIREHARNESS LIMITED , https://www.wireharness-assembling.com