Floating-point algorithms do not follow integer algorithm rules, but it is not difficult to design an accurate floating-point system using an FPGA or an FPGA-based embedded processor.
When engineers see floating-point operations, they will have a headache, because floating-point operations are slow to implement with software, and hardware implementations take up more resources. The best way to understand and understand floating point numbers is to treat them as approximations of real numbers. In fact, this is also the purpose of developing floating point expressions. As the old saying goes, the real world is analog, and there are many electronic systems dealing with real-world signals. Therefore, for engineers designing these systems, it is necessary to understand the advantages and limitations of floating-point expressions and floating-point calculations. This will help us design systems that are more reliable and fault tolerant.
First, take a deeper look at floating point arithmetic. With some example calculations, you can see that floating-point operations are not as straightforward as integer operations, and engineers must consider this when designing systems that use floating-point data. Here's an important trick: use logarithms to calculate very small floating point data. Our goal is to be familiar with the characteristics of some numerical operations and focus on design issues. A more in-depth introduction is included in the references listed at the end of this article.
For design implementations, designers can use the Xilinx LogiCORETM IP FloaTIng-Point Operator to generate and instantiate floating-point operators in RTL designs. If you are building a floating-point software system with an embedded processor in an FPGA, you can use the LogicCORE IP Virtex®-5 Auxiliary Processor Unit (APU) Floating Point Unit (FPU) for the PowerPC 440 embedded processor in the Virtex-5 FXT. .
Floating point operation 101
IEEE 754-2008 is the current IEEE standard for floating point arithmetic. (1) It replaces the IEEE 754-1985 and IEEE 754-1987 versions of the standard. The floating point data expression rules in this standard are as follows:
è¦æ±‚ Requires zero band symbol: +0,-0
ï® Non-zero floating point numbers can be expressed as (-1)^sxb^exm, where: s is +1 or -1, indicating whether the number is positive or negative, b is the base (2 or 10), and e is the exponent , m is a number expressed in the form of d0.d1d2—dp-1, where di may be 0 or 1 for the base 2, and any value between 0 and 9 for the base 10. Please note that the decimal point should be followed by d0.
ï® The limits of positive and negative: +∞,-∞.
ï® Non-numeric, there are two forms: qNaN (static) and sNaN (signal).
The expression d0.d1d2—dp-1 refers to “effective value†and e is “indexâ€. Valid values ​​have a total of p digits, and p is the precision of the expression. IEEE 754-2008 defines five basic expression formats, three for the base 2 case and two for the base 10 case. More derivative formats are also available in the standard. The single-precision floating-point and double-precision floating-point numbers specified in IEEE 754-1985 are called binary32 and binary64, respectively. A minimum index emin and a maximum exponent emax are specified for each format.
The range of finite values ​​that can be expressed in floating point format depends on the base (b), precision (p), and emax. This standard generally defines emin as 1-emax:
ï® m is an integer from 0 to b^p-1 For example, in the case of p=10 and b=2, m is between 0 and 1023.
ï® For a given number, e must satisfy the following formula
1-emax<=e+p-1<=emax
For example, if p=24 and emax=+127, the value of e ranges from -126 to 104.
It needs to be clear here that floating point expressions are often not unique.
For example, both 0.02x10^1 and 2.00x10^(-1) represent the same real number, which is 0.2. If the first digit d0 is 0, the value is said to be "normalized". Also, for a real number, there may be no floating point expressions. For example, 0.1 is a definite value in decimal, but its binary expression is an infinite loop of 0011 after the decimal point. Therefore, 0.1 cannot be definitely expressed in floating point format. Table 1 shows the five basic formats specified in IEEE 754-2008.

The error in floating-point calculations is indispensable in floating-point calculations because a fixed number of bits is used to represent an infinite number of real numbers. This inevitably introduces rounding errors, so there is a need to measure the difference between the results and the infinite precision calculation. Let's take a look at the floating point format of b=10 and p=4. In this format, .0123456 can be expressed as 1.234x10^(-2). It is clear that this expression has a .56 difference in the last position unit (ulps). For another example, if the result of the floating point calculation is 4.567x10^(-2), and the result of using the infinite precision calculation is 4.567895, the final difference is .895 the last position unit.
The "last position unit" (ulps) is a way to specify this calculation error. Relative error is another way to measure the approximate real error of a floating point number. Relative error is defined as the quotient of the difference between a real number and a floating point number divided by a real number. For example, when 4.567895 is expressed as a floating point number of 4.567x10^(-2), the relative error is .000895/4.567895≈.00019. According to the requirements of the standard, the error of the correct calculation result of each floating point number should be no more than 0.5 ulps.
Floating-point system design When designing for numerical application development, it is important to consider whether the input data or constants can be real numbers. If it can be a real number, there are some issues to be aware of before completing the design. You need to check if the values ​​from the dataset are very close in the floating-point expression, and if there is too much or too little. Let's take the root of the quadratic equation as an example. The roots α and β of the quadratic equation are expressed as the following two equations:
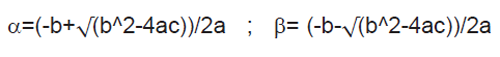
Universal Back Sticker, Back Film, TPU Back Sticker, Back Skin Sticker, PVC Back Sticker, Back Skin,Custom Phone Sticke,Custom Phone Skin,Phone Back Sticker
Shenzhen Jianjiantong Technology Co., Ltd. , https://www.jjthydrogelmachine.com