DeepMind proposed using synthetic gradients instead of back propagation to allow the network layer to learn independently and speed up training. Let's work with DeepMind Data Scientist, Udacity Deep Learning Instructor Andrew Trask, to achieve a composite gradient based on numpy.
TLDR This article will learn the intuition behind this technology by implementing DeepMind's Decoupled Neural Interfaces Using Synthetic Gradients paper from scratch.
A synthesis gradient overview
In general, neural networks compare predictions and data sets to determine how to update weights. It then uses back-propagation to find the direction in which each weight moves, making the prediction more accurate. However, in the case of Synthetic Gradient, each layer makes a "best guess" of the data, and then updates its weight according to guesses. The "best guess" is called a synthetic gradient. The data is used to help update each layer of "guessers" (composite gradient generators). In most cases, this allows the network layer to learn independently to speed up the training.
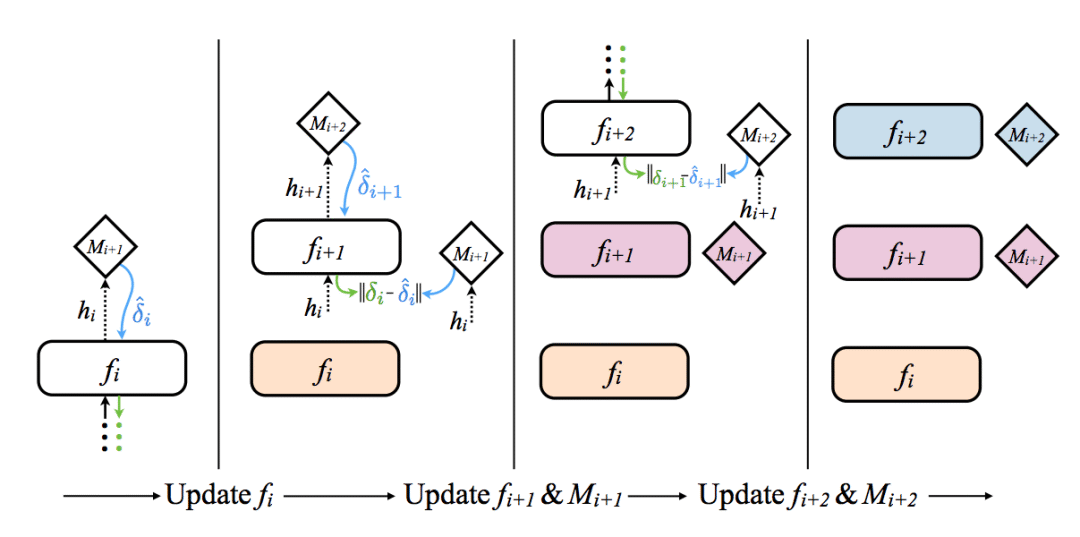
The figure above (from the paper) provides an intuitive representation (from left to right). The rounded corners are the network layer and the diamond is the synthetic gradient generator.
Second, the use of synthetic gradient
Let us briefly ignore how synthetic gradients are generated and see how they are used. The leftmost figure above shows how to update the first layer of the neural network. The first layer propagates forward to the composite gradient generator (Mi+1) and the composite gradient generator returns a gradient. The network uses this composite gradient instead of a real gradient (computing a true gradient requires a complete forward and backward propagation). Then the weights are updated as usual, pretending that the composite gradient is a true gradient. If you need to review how the weights are updated according to the gradient, please refer to my previously written Numpy-based neural network: back propagation and gradient descent.
So, in a nutshell, synthetic gradients are the same as usual gradients, and for some magical reason, they look very accurate (in the absence of viewing data)! Looks like magic? Let us see how they are generated.
Third, generate a synthetic gradient
Well, this part is very clever, and frankly, it's amazing how effective it can be. How to generate a synthetic gradient for a neural network? Well, of course you need another network! The synthetic gradient generator is nothing but a neural network trained to accept the output of a network layer and then predict the gradient of the network layer.
Side note: Related work by Geoffrey Hinton
In fact, this reminds me of Geoffrey Hinton's work a few years ago, and a random learning weights support deep learning network (arXiv: 1411.0247). Basically, you can backpropagation through a random generator matrix and still be able to complete the learning. In addition, he showed that this has some kind of regularization effect. This is definitely an interesting job.
OK, go back to the composition gradient. The paper also mentions that other relevant information can be used as input to a synthetic gradient generation network, but the paper itself seems to use only the output of the network layer as input to the generator on an ordinary feedforward network. In addition, the paper even claims that a single linear layer can be used as a synthetic gradient generator. surprising! We will try this.
How does the network learn to generate gradients?
This raises the question of how to learn how to generate synthetically gradient networks? When we perform a complete forward propagation and back propagation, we actually get a "correct" gradient. We can compare it with "synthetic" gradients, just as we usually compare neural network output with datasets. Therefore, we can pretend that "true gradients" come from a mysterious data set to train synthetic gradient networks... So we train like normal networks. Cool!
Wait a moment... If the synthetic gradient network needs to be backpropagated... what's the point?
Very good question! The full value of this technology is to allow independent training of the network layer without waiting for all network layers to complete forward propagation and reverse propagation. If the synthetic gradient network needs to wait for a complete forward/backward propagation step, we're not going back to the origin and we need to do more calculations (and worse than it was). To find the answer, let us revisit the visualization of the network architecture in the paper.
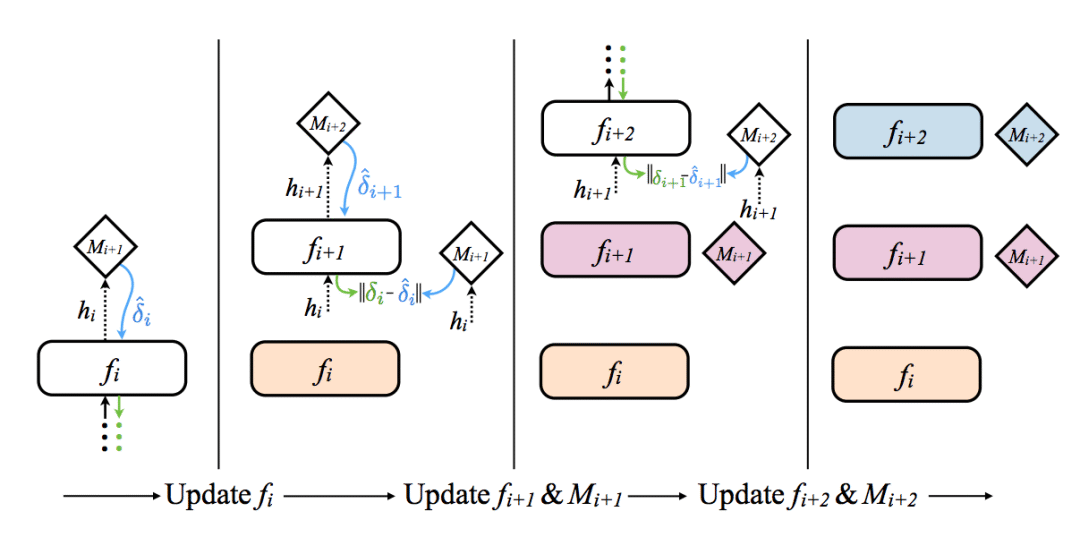
Let's focus on the second area on the left. did you see that? The gradient (Mi+2) propagates back to Mi+2 via fi+1. As you can see, each synthetic gradient generator actually uses only the synthetic gradient generated by the next layer to train. Therefore, only the last level actually trains on the data. Other layers, including synthetic gradient generation networks, are based on synthetic gradient training. Therefore, when training each layer's synthetic gradient generation network, it is only necessary to wait for the next layer's composite gradient (no other dependencies). so cool!
Fourth, the baseline neural network
It's time to write the code! I will first implement an original neural network trained by back propagation in a style similar to that of neural networks based on Numpy: Backward propagation. (So, if you have something you don't understand, you can read the articles I wrote before, and then come back to read this article). However, I will add an extra layer, but this will not cause understanding problems. I just think that since we are talking about reducing dependence, more network layers may help to form a better explanation.
As for the data set we are training, we will use binary addition to generate a composite data set (haha!). Therefore, the network will accept two random binary numbers as input and predict the sum of the two (also a binary number). This allows us to easily add dimensions (as much as difficulty) as needed. The following is the code that generates the data set.
Import numpy as np
Import sys
Def generate_dataset(output_dim = 8, num_examples=1000):
Def int2vec(x,dim=output_dim):
Out = np.zeros(dim)
Binrep = np.array(list(np.binary_repr(x))).astype('int')
Out[-len(binrep):] = binrep
Return out
X_left_int = (np.random.rand(num_examples) * 2**(output_dim - 1)).astype('int')
X_right_int = (np.random.rand(num_examples) * 2**(output_dim - 1)).astype('int')
Y_int = x_left_int + x_right_int
x = list()
For i in range(len(x_left_int)):
X.append(np.concatenate((int2vec(x_left_int[i]), int2vec(x_right_int[i]))))
y = list()
For i in range(len(y_int)):
Y.append(int2vec(y_int[i]))
x = np.array(x)
y = np.array(y)
Return (x,y)
Num_examples = 1000
Output_dim = 12
Iterations = 1000
x,y = generate_dataset(num_examples=num_examples, output_dim = output_dim)
Print("Input: two concatenated binary values:")
Print(x[0])
Print("Output: binary value of their sum:")
Print(y[0])
The following is the corresponding neural network code:
Batch_size = 10
Alpha = 0.1
Input_dim = len(x[0])
Layer_1_dim = 128
Layer_2_dim = 64
Output_dim = len(y[0])
Weights_0_1 = (np.random.randn(input_dim,layer_1_dim) * 0.2) - 0.1
Weights_1_2 = (np.random.randn(layer_1_dim,layer_2_dim) * 0.2) - 0.1
Weights_2_3 = (np.random.randn(layer_2_dim,output_dim) * 0.2) - 0.1
For iter in range(iterations):
Error = 0
For batch_i in range(int(len(x) / batch_size)):
Batch_x = x[(batch_i * batch_size):(batch_i+1)*batch_size]
Batch_y = y[(batch_i * batch_size):(batch_i+1)*batch_size]
Layer_0 = batch_x
Layer_1 = sigmoid(layer_0.dot(weights_0_1))
Layer_2 = sigmoid(layer_1.dot(weights_1_2))
Layer_3 = sigmoid(layer_2.dot(weights_2_3))
Layer_3_delta = (layer_3 - batch_y) * layer_3 * (1 - layer_3)
Layer_2_delta = layer_3_delta.dot(weights_2_3.T) * layer_2 * (1 - layer_2)
Layer_1_delta = layer_2_delta.dot(weights_1_2.T) * layer_1 * (1 - layer_1)
Weights_0_1 -= layer_0.T.dot(layer_1_delta) * alpha
Weights_1_2 -= layer_1.T.dot(layer_2_delta) * alpha
Weights_2_3 -= layer_2.T.dot(layer_3_delta) * alpha
Error += (np.sum(np.abs(layer_3_delta)))
Sys.stdout.write("Iter:" + str(iter) + " Loss:" + str(error))
If(iter % 100 == 99):
Print("")
Now, I really feel that it is necessary to do something I almost never do when I study, plus a little object-oriented structure. Usually, this will slightly confuse the network and make it harder to see what the code does. However, since the subject of this article is "Decoupled Neural Interfaces" and their advantages, it would be quite difficult to explain without decoupling these interfaces. Therefore, I will convert the above network into a Layer class, which will be further converted to a DNI (Decoupled Network Interface).
classLayer(object):
Def __init__(self,input_dim,output_dim,nonlin,nonlin_deriv):
Self.weights = (np.random.randn(input_dim, output_dim) * 0.2) - 0.1
Self.nonlin = nonlin
Self.nonlin_deriv = nonlin_deriv
Def forward(self,input):
Self.input = input
Self.output = self.nonlin(self.input.dot(self.weights))
Return self.output
Def backward(self,output_delta):
Self.weight_output_delta = output_delta * self.nonlin_deriv(self.output)
Return self.weight_output_delta.dot(self.weights.T)
Def update(self,alpha=0.1):
Self.weights -= self.input.T.dot(self.weight_output_delta) * alpha
In this Layer class, we have some variables. The weights are the matrix that we transform linearly from input to output (just like the usual linear layer). We also introduced an output nonlin function that adds nonlinearity to our network output. If we don't want nonlinearity, we can set its value directly to lambda x:x. In our case, we will pass in the sigmoid function.
The second function we pass in is nonlin_deriv, which is a derivative. This function will accept our nonlinear output and convert it to a derivative. For sigmoids, its value is (out * (1 - out)), where out is the output of sigmoid.
Now let's look at some of the methods in the class. Forward, as the name suggests, forward propagation, first through a linear transformation followed by a nonlinear function. Backward accepts an output_delta parameter that represents the true gradient (non-composite gradient) returned from the next layer back propagation. We then use this parameter to calculate self.weight_output_delta, which is the derivative of the weight output. Finally, the error sent back to the previous layer is back-propagated and the error is returned.
Update is perhaps the simplest function. It directly accepts the derivative of the weighted output and uses it to update the weights. If you do not understand any of the steps, please refer to Numpy-based neural network again: Backward propagation.
Next, let's see how the layer object is used for training.
Layer_1 = Layer(input_dim,layer_1_dim,sigmoid,sigmoid_out2deriv)
Layer_2 = Layer(layer_1_dim, layer_2_dim, sigmoid, sigmoid_out2deriv)
Layer_3 = Layer(layer_2_dim, output_dim, sigmoid, sigmoid_out2deriv)
For iter in range(iterations):
Error = 0
For batch_i in range(int(len(x) / batch_size)):
Batch_x = x[(batch_i * batch_size):(batch_i+1)*batch_size]
Batch_y = y[(batch_i * batch_size):(batch_i+1)*batch_size]
Layer_1_out = layer_1.forward(batch_x)
Layer_2_out = layer_2.forward(layer_1_out)
Layer_3_out = layer_3.forward(layer_2_out)
Layer_3_delta = layer_3_out - batch_y
Layer_2_delta = layer_3.backward(layer_3_delta)
Layer_1_delta = layer_2.backward(layer_2_delta)
Layer_1.backward(layer_1_delta)
Layer_1.update()
Layer_2.update()
Layer_3.update()
If you compare the above code with the previous one, basically everything happens in basically the same place. I just replaced the corresponding action in the script with the method call.
So, what we actually do is extract the steps from the previous script and divide it into different functions in the class.
If you do not understand this new version of the network, do not continue. Make sure you are accustomed to this kind of abstraction before continuing reading below, because the following will become more complicated.
Fifth, the synthetic gradient based on layer output
Now we will rewrite the Layer class based on the knowledge of the synthesized gradient and rename it DNI.
Class DNI(object):
Def __init__(self,input_dim,output_dim,nonlin,nonlin_deriv,alpha = 0.1):
# as before
Self.weights = (np.random.randn(input_dim, output_dim) * 0.2) - 0.1
Self.nonlin = nonlin
Self.nonlin_deriv = nonlin_deriv
# New thing
Self.weights_synthetic_grads = (np.random.randn(output_dim,output_dim) * 0.2) - 0.1
Self.alpha = alpha
# Just before `forward`, we now update weights based on synthetic gradients in forward propagation
Def forward_and_synthetic_update(self,input):
# Cache input
Self.input = input
# Forward propagation
Self.output = self.nonlin(self.input.dot(self.weights))
# Generate a synthetic gradient based on a simple linear transformation
Self.synthetic_gradient = self.output.dot(self.weights_synthetic_grads)
# Update weights using synthetic gradients
Self.weight_synthetic_gradient = self.synthetic_gradient * self.nonlin_deriv(self.output)
Self.weights += self.input.T.dot(self.weight_synthetic_gradient) * self.alpha
# Returns the backward propagated composite gradient (this is similar to the output of the backprop method of the Layer class)
# Also return forward-propagation output (I know this is a bit weird...)
Return self.weight_synthetic_gradient.dot(self.weights.T), self.output
# is similar to the previous `update` method except that it is based on composition weights
Def update_synthetic_weights(self, true_gradient):
Self.synthetic_gradient_delta = self.synthetic_gradient - true_gradient
Self.weights_synthetic_grads += self.output.T.dot(self.synthetic_gradient_delta) * self.alpha
We have some new variables. The only key is self.weights_synthetic_grads, which is our synthetic gradient generator neural network (just a linear layer...that is...a matrix).
Forward propagation and synthesis update: The forward method becomes forward_and_synthetic_update. Remember that we don't need the rest of the network to update weights? This is where the magic happens. First, forward propagation is performed as usual. Next, we generate a composite gradient by passing the output to a non-linearity. This part could have been a more complex neural network, but we didn't do it but decided to keep it simple and use a simple linear layer to generate our composite gradient. After getting our gradient, we continue to update the weights. Finally, we propagate the synthesized gradient back so that it can be sent to the previous layer.
Update composition gradient: The update_synthetic_gradient method of the next layer will accept the gradient returned by the forward_and_synthetic_update method of the previous layer. So, if we are in the second layer, then the gradient returned by the third layer's forward_and_synthetic_update method will be the input to the second layer's update_synthetic_weights. Then, we update the composition weights directly, just as we did in ordinary neural networks. This is no different from the usual neural network learning, except that we use some special input and output.
Based on the synthetic gradient method to train the network, I found that it did not converge as I expected. I mean, it's convergence, but it's very slow. I took a closer look and found that the hidden representation (that is, the gradient generator's input) was initially flat and random. In other words, two different training samples will have almost the same output representation at different network layers. This greatly increases the difficulty of working with gradient generators. In the paper, the solution the author used was batch normalization, batch normalization scaling all network layer outputs to zero mean and unit variance. In addition, the paper mentions that you can use other forms of gradient generator input. For our simple toy neural network, batch normalization adds a lot of complexity. Therefore, I tried to use the output data set. This did not undermine the decoupled state (upholding the spirit of DNI), but it provided very powerful information to the network at the beginning.
After making this change, training is much faster! It is a fascinating activity to think about what can act as a good input to a gradient generator. Maybe some combination of input data, output data, batch normalization layer output would be the best (welcome to try!) Hope you enjoy this tutorial.
Copper Tube Terminals Without Checking Hole
Our company specializes in the production and sales of all kinds of terminals, copper terminals, nose wire ears, cold pressed terminals, copper joints, but also according to customer requirements for customization and production, our raw materials are produced and sold by ourselves, we have their own raw materials processing plant, high purity T2 copper, quality and quantity, come to me to order it!
Copper Tube Terminals Without Checking Hole,Cable Lugs Insulating Crimp Terminal,Cable Connector Tinned Copper Ring Terminal,Tubular Cable Lugs Crimp Terminal
Taixing Longyi Terminals Co.,Ltd. , https://www.lycopperlugs.com